这篇博客主要为了整理 \(\mathbb{R}^n\) 上开集、闭集等各种基本概念和性质，然后过渡到距离空间的开集概念，进一步抽象到拓扑空间的相关概念，这篇博客涉及到的命题、性质等摘自基本的数学分析教材、点集拓扑教材等，主要目的是整理这些概念及其相互关系。

一、引入

设 \(a \in \mathbb{R}^n\), \(r>0\), 定义：
（开球） \(B(a;r) = \lbrace x \in \mathbb{R}^n: \lVert x-a \rVert < r \rbrace\)
（闭球） \(\bar{B}(a;r) = \lbrace x \in \mathbb{R}^n: \lVert x-a \rVert \le r \rbrace\)
（球面） \(S(a,r) = \lbrace x \in \mathbb{R}^n: \lVert x-a \rVert = r \rbrace\)

二、开集

定义2.1（开集） \(E\subset \mathbb{R}^n\) 是开集，若对任意的 \(a\in E\), 存在 \(r>0\), 使得 \(B(a;r) \subset E\).
例1：\(E = \mathbb{R}^n-\lbrace a \rbrace\)（即 \(\mathbb{R}^n\) 挖去任一个点构成的集合） 是开集。
可以推广：\(\mathbb{R}^n\) 挖去任意有限个点构成的集合仍然是开集。
例2： 开球 \(B(a;r)\) 是开集。
例3：开区间 \((a,b)\) 是 \(\mathbb{R}^1\) 中的开集，不是 \(\mathbb{R}^2\) 中的开集。（该例主要为了厘清开集的概念）

下面给出 \(\mathbb{R}^n\) 中开集的基本性质，也是以后定义拓扑的基本出发点。
定理2.2（开集基本性质） 在空间 \(\mathbb{R}^n\) 中，
(1) \(\mathbb{R}^n\), \(\emptyset\) 是开集；
(2) 任意多个开集的并是开集；
(3) 有限多个开集的交是开集。
注：定理2.2(3)中开集的个数必须是有限个，见反例: \[\bigcap\limits_{i=1}^\infty B(0;1/i) = \lbrace 0\rbrace\]

三、闭集的第一种定义方式

开始给出闭集最基本的定义，通过开集来刻画。
定义3.1（闭集） 设 \(F\subset \mathbb{R}^n\). 若 \(F\) 的补集 \(F^c\) 是开集， 则称 \(F\) 是闭集。
类似开集的基本性质，我们有：
定理3.2（闭集基本性质） 在空间 \(\mathbb{R}^n\) 中，
(1) \(\mathbb{R}^n\), \(\emptyset\) 是闭集；
(2) 任意多个闭集的交是闭集；
(3) 有限多个闭集的并是闭集。
注：无穷多个闭集的并不一定是闭集， 比如取 \(\mathbb{R}^1\) 中的闭集 \(F_k = [\frac{1}{k+1},\frac{1}{k}]\), 则有 \[\bigcup\limits_{k=1}^\infty F_k = (0,1].\]

例4：由例1知，除去 \(\mathbb{R}^n\) 中的有限多个点所成的集合是开集，则 \(\mathbb{R}^n\) 中有限个点所成的集合是闭集。
例5：在 \(\mathbb{R}^n\) 中，开球的补集是闭集。

四、闭集的第二种定义方式：引入聚点，导集， 闭包

定义4.1（聚点） 设 \(E\subset \mathbb{R}^n\). 若点 \(x \in \mathbb{R}^n\) 有这样的性质：对任意的 \(r>0\), \(B(x;r)\) 中至少含有 \(E\) 中异于 \(x\) 的一个点 \(y\)，即 \(B(x;r)\cap (E - \lbrace x \rbrace) \ne \emptyset\). 则称 \(x\) 为 \(E\) 的聚点（或极限点）。
记 \(E^\prime = \lbrace E\text{的所有极限点}\rbrace\), 称其为 \(E\) 的导集。
注：
1) \(x\in E^\prime\) \(\Leftrightarrow\) \(\forall r>0\), \(B(x;r)\) 中至少含有 \(E\) 中一个点 \(y \ne x\).
                \(\Leftrightarrow\) \(\forall r>0\), \(B(x;r)\) 含有 \(E\) 中无穷多个点。
2) \(x \notin E^\prime\) \(\Leftrightarrow\) \(\exists r>0\), s.t. \(B(x;r) \cap (E - \lbrace x \rbrace) = \emptyset\).
                \(\Leftrightarrow\) \(\exists r > 0\), 使得 \(B(x;r)\) 最多只有 \(E\) 中有限多个点。

接下来用 \(E\) 中序列极限的观点来看聚点，正如聚点的另一名称：极限点。
定理4.2 设 \(E\subset \mathbb{R}^n\)， 则下列三个命题等价：
(i) \(x \in E^\prime\);
(ii) 存在点列 \(\lbrace x_k \rbrace\) 满足 \(x_k \in E\), \(x_k \ne x\quad(k=1,2,\cdots)\), 使得 \(x_k \rightarrow x \ (k \rightarrow \infty)\);
(iii) 存在 \(E\) 中的互异点列 \(\lbrace x_k \rbrace\)， 使得 \(x_k \rightarrow x \ (k \rightarrow \infty)\).
具体证明见：https://swt-2020.github.io/open_set/Thm_4.2.pdf [自动忽略字写的比较丑(つェ⊂！)]
注：
1) 有限集不存在聚点。
2) \(E\) 的聚点不一定在 \(E\) 中，如在 \(\mathbb{R}^1\) 中取 \(E = (0,1)\), 则\(E^\prime = [0,1]\), 但0，1不在 \(E\) 中。
3) 若 \(E\) 中的点 \(x\) 不是 \(E\) 的聚点，即 \(x \in E-E^\prime\), 则称 \(x\) 为 \(E\) 的孤立点。 \(E-E^\prime = \lbrace E \text{的所有孤立点}\rbrace\)，记其为 \(E\) 的孤立点集。 如取 \(E = \lbrace 1,\frac12,\cdots,\frac1k,\cdots\rbrace\)，则 \(E^\prime = \lbrace 0\rbrace\), 且一切 \(\frac1k (k=1,2,\cdots)\)均为 \(E\)的孤立点。
4) \(\mathbb{N}^\prime = \emptyset\), \(\mathbb{Z}^\prime = \emptyset\), \(\mathbb{Q}^\prime = \mathbb{R}\), \((\mathbb{R}-\mathbb{Q})^\prime = \mathbb{R}\), \(\mathbb{R}^\prime = \mathbb{R}\).

性质4.3（导集运算性质） 设 \(A,B \subset \mathbb{R}^n\)，则
1）\(\emptyset^\prime = \emptyset\);
2) \(A\subset B\) \(\Rightarrow\) \(A^\prime \subset B^\prime\);
3) \((A\cup B)^\prime = A^\prime \cup B^\prime\);\(\quad\) \((A\cap B)^\prime \subset A^\prime \cap B^\prime\);
4) \((A^\prime)^\prime \subset A \cup A^\prime\).
具体证明见：https://swt-2020.github.io/open_set/Prop_4.3.pdf
注：3)和4)的包含关系取不到等号，构造如下两个例子：
例3)-1：在 \(\mathbb{R}\) 中，取 \(A=[0,1)\), \(B=(1,2]\), 则 \(A^\prime = [0,1]\), \(B^\prime = [1,2]\), 但 \(A\cap B = \emptyset\).
例4)-2：在 \(\mathbb{R}\) 中，取 \(A=[0,1)\cup \lbrace 2\rbrace\), 则 \(A^\prime = [0,1]\), \((A^\prime)^\prime = [0,1]\).

接下来通过导集定义闭集的概念。
定理4.4 设 \(E \subset \mathbb{R}^n\), 则 \(E\) 是闭集 的充要条件是 \(E^\prime \subset E\) (即 \(E\) 包含 \(E\) 的一切聚点)。
注：
1) 有限点集 \(E\) 是闭集， 这时 \(E^\prime = \emptyset\).
2) 孤立点集不一点是闭集，如 \(E = \lbrace 1,\frac12,\cdots,\frac1k,\cdots\rbrace\)，这时 \(E^\prime = \lbrace 0\rbrace\).
3) 对任意集合 \(E\subset \mathbb{R}^n\), \(E\) 的导集 \(E^\prime\)是闭集。

（重要！！！）用收敛点列的极限来刻画闭集概念，这也是分析过程中最常用的验证技巧。
定理4.5 设 \(E \subset \mathbb{R}^n\), 则 \(E\) 是闭集 当且仅当 \(E\) 中的任何收敛点列的极限必在 \(E\) 中。
（换一种等价形式：\(E\) 中的序列 \(\lbrace x_k \rbrace\) 若收敛到 \(x\) 时，则有 \(x \in E\)）.
具体证明见：https://swt-2020.github.io/open_set/Thm_4.5.pdf

五、闭包基本概念

定义5.1 设 \(E \subset \mathbb{R}^n\), 记 \(\overline{E} = E \cup E^\prime\), 称 \(\bar{E}\) 为 \(E\) 的闭包（ 由定理4.4可知，\(E\) 为闭集 当且仅当 \(E = \overline{E}\)）。
注：
1) \(E \subset \overline{E}\).
2) \(\overline{\mathbb{Q}} = \mathbb{R}\), \(\overline{\mathbb{R}-\mathbb{Q}} = \mathbb{R}\).
3) \(\mathbb{R}^n\) 中开球 \(B(a;r)\) 的闭包是 闭球\(\overline{B}(a;r)\); 从而 \(\mathbb{R}^n\) 中球面 \(S(a,r)\) 是闭集。

下面描述闭包的本质特征：
定理5.2（闭包的本质特征） 对任意集合 \(E\subset \mathbb{R}^n\),
(1) \(E\) 的闭包 \(\overline{E}\) 都是闭集;
(2) \(E\) 的闭包等于包含 \(E\) 的所有闭集之交，换言之，\(\overline{E}\) 是包含 \(E\) 内的最小闭集。

性质5.3（闭包运算性质） 设 \(A,B\subset \mathbb{R}^n\)， 则
1) \(\overline{\emptyset} = \emptyset\);
2) \(A\subset B\) \(\Rightarrow\) \(\overline{A} \subset \overline{B}\);
3) \(\overline{A\cup B} = \overline{A}\cup \overline{B}\) \(\quad\) \(\overline{A\cap B} \subset \overline{A}\cap \overline{B}\);
4) \(\overline{\overline{A}} = \overline{A}\).
具体证明见：https://swt-2020.github.io/open_set/Prop_5.3.pdf
注：3)的包含关系取不到等号，构造如下例子：
在 \(\mathbb{R}\) 中，取 \(A=[0,1)\), \(B=(1,2]\), 则 \(\overline{A} = [0,1]\), \(\overline{B} = [1,2]\), 但 \(A\cap B = \emptyset\).

接下来（重点！！！）用收敛点列的极限来刻画闭包概念：
定理5.4 设 \(E\subset \mathbb{R}^n\), 则 \(x \in \overline{E}\) 当且仅当 存在 \(E\) 中的一个序列 \(\lbrace x_k\rbrace\), 它收敛到 \(x\).
（换一种等价形式： 对任意 \(r>0\), 有 \(B(x;r) \cap E \ne \emptyset\).）
具体证明见：https://swt-2020.github.io/open_set/Thm_5.4.pdf
注： \(x \notin \overline{E}\) 当且仅当 存在一个 \(r>0\), 使得 \(B(x;r) \cap E = \emptyset\).

六、内点、外点以及边界点

设点集 \(E\subset \mathbb{R}^n\)，对任意 \(x\in \mathbb{R}^n\), 有下面三种情况：
(1) 内点 存在 \(r>0\)，使得 \(B(x;r) \subset E\)， 则称 \(x\) 为 \(E\) 的一个内点。
     记 \(E^o = \lbrace E\text{的所有内点}\rbrace\), 称其为 \(E\) 的内部。
(2) 外点 存在 \(r>0\)，使得 \(B(x;r)\) 完全不落在 \(E\) 中，即 \(B(x;r) \subset E^c\), 这时称 \(x\) 为 \(E\) 的一个外点，也可以说 \(x\) 为 \(E^c\) 的一个内点。
     从而 \((E^c)^o = \lbrace E\text{的所有外点}\rbrace\), 称其为 \(E\) 的外部。
(3) 边界点 既不是 \(E\) 的内点又不是 \(E\) 的外点的点称为 \(E\) 的边界点，换言之， 对任意 \(r>0\), \(B(x;r)\) 既包含 \(E\) 中的点，又包含 \(E^c\) 中的点。
     记 \(\partial E = \lbrace E\text{的边界点的全体}\rbrace\)，称其为 \(E\) 的边界。

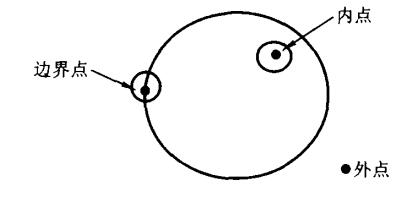
注：
1) \(E^o \subset E\)； 从开集的定义2.1知，\(E\) 为开集 当且仅当 \(E = E^o\).
2) 内点必属于 \(E\), 外点必属于 \(E^c\), 但边界点可能属于 \(E\), 也可能不属于 \(E\).
3) 孤立点必是边界点。 [回顾孤立点定义：若 存在 \(r>0\)，使得 \(B(x;r)\) 中只有 \(x\) 点属于 \(E\).]
4) 对一切集 \(E\subset \mathbb{R}^n\)， \(E^o\), \((E^c)^o\) 与 \(\partial E\)互不相交，并且 \(\mathbb{R}^n = E^o \cup (E^c)^o \cup \partial E.\)

例6： 若 \(E \subset \mathbb{R}^n\), 则 \(E^o = E\), \((E^c)^o = \partial E =\emptyset\).
例7： 设单点集 \(E = \lbrace a \rbrace\), 则 \(E^o = \emptyset\), \((E^c)^o = E^c\), \(\partial E = E\).
例8： 设 \(E = B(a;r)\), 则 \(E^o = E\), \((E^c)^o = \lbrace x\in \mathbb{R}^n: \lVert x-a \rVert > r \rbrace\), \(\partial E = S(a,r) = \lbrace x \in \mathbb{R}^n: \lVert x-a \rVert = r \rbrace\).

接下来给出点集 \(E\) 的内部和闭包的联系， 这个定理非常重要，意味着关于内部的基本性质和闭包的性质完全对偶，可以互相转化。
定理6.1（重要！！！） 设点集 \(E \subset \mathbb{R}^n\)， 则 \(E^o = \big(\overline{E^c}\big)^c\), 以及 \(\overline{E} = ((E^c)^o)^c\).
具体证明见：https://swt-2020.github.io/open_set/Thm_6.1.pdf

由定理6.1 内部和闭包成对偶关系，可将定理5.2、性质5.3简单转化成内部所具有的性质。
定理6.2（内部的本质特征） 对任意集合 \(E\subset \mathbb{R}^n\),
(1) \(E\) 的内部 \(E^o\) 是开集;
(2) 设 \(\mathcal{T}\) 是由 \(\mathbb{R}^n\) 中所有开集构成的集族， 则 \[ E^o = \bigcup\limits_{F\in \mathcal{T},F\subset E}F \] 即 \(E\) 的内部等于包含于 \(E\) 的所有开集之并，换言之，\(E^o\) 是包含于 \(E\) 内的最大开集。

性质6.3（内部运算性质） 设 \(A,B\subset \mathbb{R}^n\)， 则
1）\((\mathbb{R}^n)^o = \mathbb{R}^n\);
2) \(A\subset B\) \(\Rightarrow\) \(A^o \subset B^o\);
3) \((A\cap B)^o = A^o \cap B^o\), \(\quad\) \(A^o \cup B^o \subset (A\cup B)^o\);
4) \((A^o)^o = A^o\).
具体证明见：https://swt-2020.github.io/open_set/Prop_6.3.pdf
注：3)的包含关系取不到等号，构造如下例子：
在 \(\mathbb{R}\) 中，取 \(A=(0,1]\), \(B=[1,2)\), 则 \(A^o = (0,1)\), \(B^o = (1,2)\), 但 \(A\cup B = (0,2)\).

关于闭包，内部，边界之间存在着种种联系，列举如下：
定理6.4 设点集 \(A, B \subset \mathbb{R}^n\)，则
(1) \(\partial A = \overline{A} \cap \overline{A^c}= (A^o \cup (A^c)^o)^c = \partial A^c\);
(2) \(\overline{A} = A^o\cup \partial A\) （不交并）， \(A^o = \overline{A} - \partial A\), \(\partial A = \overline{A} - A^o\), 以及 \(\partial A\) 是闭集;
(3) \(\overline{A} = A\cup \partial A\) ， \(A^o = A - \partial A\);
(4) \(\partial A^o \subset \partial A\), \(\partial \overline{A} \subset \partial A\);
(5) \(\partial (A\cup B) \subset \partial A \cup \partial B\);
(6) \(\partial (\partial A) \subset \partial A\);
(7) \(\partial A = \emptyset\) 当且仅当 \(A\) 既开又闭;
(8) \(A\) 为闭集 当且仅当 \(\partial A \subset A\).
\(\ \ \ \ \) \(A\) 为开集 当且仅当 \(A \cap \partial A = \emptyset\)
具体证明见：https://swt-2020.github.io/open_set/Thm_6.4.pdf

七、紧集（Compact Set）

对点集 \(E\subset \mathbb{R}^n\), 令 \[ diam(E) = \sup\lbrace \lVert x-y \rVert:x,y\in E\rbrace,\] 称 \(diam(E)\) 为点集 \(E\) 的 直径。
若 \(diam(E)< +\infty\),则称 \(E\) 为有界集。
注：（另一种定义方式） \(E\) 是有界集 当且仅当 存在 \(M>0\), 使得对 \(\forall x\in E\), 都满足 \(\lVert x \rVert \le M\).

定义7.1 设 \(E\subset \mathbb{R}^n\)，\(\mathcal{I} = \lbrace G_{\alpha} \rbrace\) 是 \(\mathbb{R}^n\) 中的一个开集族。 如果 \[ E\subset \bigcup\limits_{\alpha} G_{\alpha},\] 则称开集族 \(\mathcal{I}\) 覆盖了 \(E\), 或者称 \(\mathcal{I}\) 构成 \(E\) 的一个开覆盖。
若能从 \(E\) 的任一个开覆盖中选出有限个开集， 仍然构成 \(E\) 的开覆盖，则称 \(E\) 是一个紧致集。
注：
1) \(\mathcal{I} = \lbrace G_{\alpha} \rbrace\) 覆盖了 \(E\) 意思是：对任意 \(x\in E\), 必存在一个开集 \(G_{\alpha} \in \mathcal{I}\), 使得 \(x \in G_{\alpha}\).
2) \(E\) 是一个紧致集: 对 \(E\) 的任一个开覆盖 \(\mathcal{I} = \lbrace G_{\alpha} \rbrace\)，存在 \(\mathcal{I}\) 中有限个开集 \(\lbrace G_{\alpha_i} \rbrace_{i=1}^p\) 满足 \(E \subset \bigcup\limits_{i=1}^p G_{\alpha_i}\).

定义7.2 设 \(E\subset \mathbb{R}^n\). 如果 \(E\) 中的任一点列都有一收敛子列，且该子列收敛到 \(E\) 中一点，则称 \(E\) 是 \(\mathbb{R}^n\) 中的一个列紧集。

定理 设 \(E\subset \mathbb{R}^n\)，则下述三个命题等价：
(1) \(E\) 是有界闭集；
(2) \(E\) 是紧致集；
(3) \(E\) 是列紧集。

注：
1) 在 设 \(\mathbb{R}^n\) 中， 列紧集和紧致集二者等价，统称为紧集；
2) \(\mathbb{R}^n\) 中 的紧集即是有界闭集。