前几节分别介绍了凸集、仿射集 和 锥 等概念和一些运算性质，这节在此基础上进一步研究凸集常用的性质。

一、 Caratheodory 定理

这一部分介绍凸几何上关于凸包的常用性质，如下：
定理1.1 （Caratheodory 定理【凸包】） 设集合 $C \subset \mathbb{R}^n$, 则凸包 $\mathrm{conv}(C)$ 中任意一点 $x$ 都可以表示成 $C$ 中至多 $n+1$ 个点的凸组合。（用符号表示：$\forall x\in \mathrm{conv}(C)$, 则 $x = \sum_{i=1}^{n+1} \alpha_i x_i$,其中 $\alpha_i\ge 0, x_i\in C,i=1,\cdots,n+1$, $\sum_{i=1}^{n+1}\alpha_i = 1$.）
注：
1) 由凸包定义可知，凸包 $\mathrm{conv}(C)$ 中任意一点都可以表示成 $C$ 中任意有限个点的凸组合，而Caratheodory 定理将其有限个点的范围控制在至多有 $n+1$ 个点的凸组合。
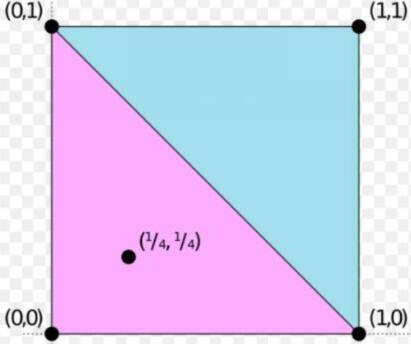
2) 下图给出刻画上述定理的一个图示，设 $C = \lbrace (0,0),(0,1),(1,0),(1,1)\rbrace$ 是 $\mathbb{R}^2$ 的子集，则 $\mathrm{conv}(C)$ 为下图中的正方形，考虑 $x=(\frac14,\frac14)$, 则 $x$ 可以表示为 $(0,0),(0,1),(1,0)$ 的凸组合。

对锥包 $\mathrm{cone}(C)$ 而言，也有类似定理1.1的结论，即对锥包而言的Caratheodory 定理。
定理1.2（Caratheodory 定理【锥包】） 设集合 $C \subset \mathbb{R}^n$, 则锥包 $\mathrm{cone}(C)$ 中任意一点 $x$ 都可以表示成 $C$ 中至多 $n$ 个点的锥组合。 （用符号表示：$\forall x\in \mathrm{conv}(C)$, 则 $x = \sum_{i=1}^{n} \alpha_i x_i$,其中 $\alpha_i\ge 0, x_i\in C,i=1,\cdots,n$.）

推论1.3 紧集的凸包仍然是紧集。

注： 闭集的凸包不一定是闭集，见反例如下：
取 $\mathbb{R}^2$ 中的闭集 $A = \lbrace(0,0)\rbrace \cup \lbrace (x_1,x_2)|x_1x_2 \ge 1,x_1\ge 0,x_2\ge 0\rbrace$. 则

$$\mathrm{conv}(A) = \lbrace(0,0)\rbrace \cup \lbrace (x_1,x_2)|x_1> 0,x_2> 0\rbrace.$$ 显然 $A$ 是闭集，然而 $\mathrm{conv}(A)$ 不是闭集。

二、 投影定理

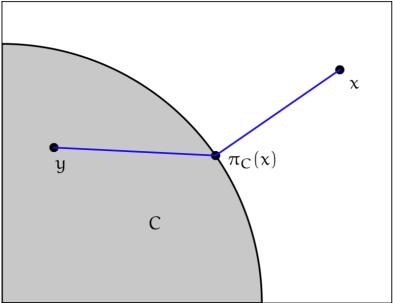
定理2.1（投影定理） 设集合 $C$ 是 $\mathbb{R}^n$ 中的非空闭凸集。
(1) 对 $\forall x\in \mathbb{R}^n$, 存在唯一的点 $\pi_C (x)\in C$, 使得

$$\lVert x-\pi_C (x)\rVert_2 = \inf_{y\in C} \lVert x - y\rVert_2.$$ 称 $\pi_C (x)$ 是 $x$ 到 $C$ 上的投影.
(2) 对 $\forall x\in \mathbb{R}^n$, 则点 $z = \pi_C (x)$ 是 $x$ 到 $C$ 的投影 当且仅当 $\forall y \in C$ 有 $\langle x-z,y-z\rangle \le 0$.
(3) 将 $\pi_C$ 看成映射 $\pi_C:\mathbb{R}^n\to C$，则 $\pi_C$ 是连续且非扩张的，即 $\lVert \pi_C (x) - \pi_C (y)\rVert \le \lVert x-y\rVert,\ \ \ \forall x,y\in \mathbb{R}^n$.

三、凸集分离定理

在介绍凸集分离定理之前，先引入超平面、半空间等概念。
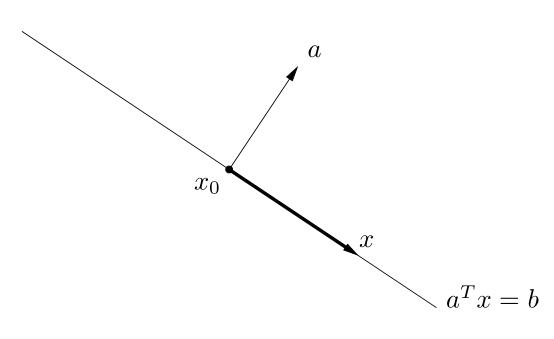
1.超平面: $\mathcal{H} = \lbrace x| a^Tx = b\rbrace$, 其中 $a\in \mathbb{R}^n, a\ne 0\rbrace$ 且 $b\in \mathbb{R}$.
几何解释：对 $\forall x_o \in \mathcal{H}$, 则超平面可表示成下面一种形式：

$$\mathcal{H} = \lbrace x|a^T(x-x_0)=0\rbrace = x_0 + a^\perp, \text{其中} a^\perp=\lbrace v|a^Tv=0\rbrace,$$ 可以看出超平面由 $x_0$ 加上所有正交于法向量 $a$ 的向量构成。
下图刻画 $\mathbb{R}^2$ 中的超平面：

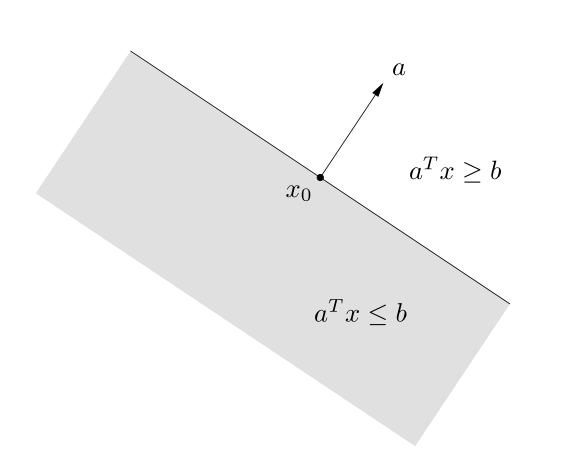
2.半空间: 一个超平面将 $\mathbb{R}^n$ 划分成两个(闭)半空间，即

$$\mathcal{H}^+ = \lbrace x| a^Tx \ge b\rbrace, \ \ \ \ \ \ \mathcal{H}^- = \lbrace x| a^Tx \le b\rbrace,$$ 其中 $a\ne 0$.（至于开半空间无非将上述闭半空间中去掉等号即可。）

定义3.1（分离超平面） 设 $\mathbb{R}^n$ 中两个不相交的非空集合 $C$ 和 $D$, 即 $C\cap D = \emptyset$, 若存在 $a\ne 0$ 和 $b$ 使得

$$a^Tx\le b,\forall x\in C;\ \ \ a^Tz \ge b, \forall z\in D.$$ 则称超平面 $\mathcal{H} = \lbrace x| a^Tx = b\rbrace$ 分离集合 $C$ 和 $D$.

定理3.2（凸集分离定理） 设 $C$ 和 $D$ 是 $\mathbb{R}^n$ 中两个不相交的非空凸集, 则存在超平面将 $C$ 和 $D$ 分离。

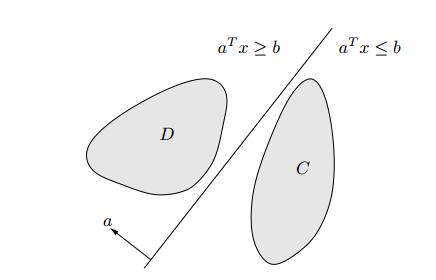
定义3.3（严格分离超平面）若定义3.1中构造的超平面满足更强的条件，即存在 $a\ne 0$ 和 $b$ 使得

$$a^Tx< b,\forall x\in C;\ \ \ a^Tz > b, \forall z\in D,$$ 则称超平面 $\mathcal{H} = \lbrace x| a^Tx = b\rbrace$ 严格分离集合 $C$ 和 $D$.
注： 一般情况下，两个不相交的凸集不一定能够被超平面严格分离，即使是闭凸集的情况，也不一定可以严格分离。见反例如下：
取 $\mathbb{R}^n$ 中的集合 $C = \lbrace (x,y)|xy\ge 1,x,y>0$, $D = \lbrace (x,y)|x\le 0\rbrace$ 即可。

命题3.4 设 $C$ 和 $D$ 是两个不相交的非空闭凸集，且二者至少有一个是紧集，则存在超平面严格分离 $C$ 和 $D$.

命题3.5（点和闭凸集的严格分离） 设 $C\subset \mathbb{R}^n$ 是闭凸集，$x_0\notin C$, 则存在超平面严格分离 $x_0$ 和 $C$.

推论3.6 任意一个闭凸集 $C$ 都是包含它的所有半空间的交：

$$C = \bigcap \lbrace \mathcal{H}|\mathcal{H}\text{是半空间}，C\subset \mathcal{H}\rbrace.$$

四、支撑超平面定理

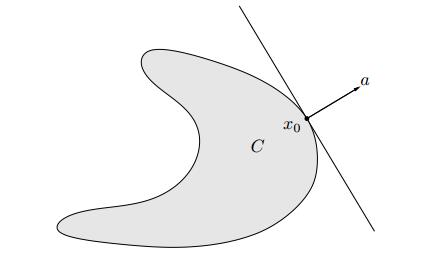
定理4.1（支撑超平面定理） 设 $C\subset \mathbb{R}^n$ 是非空凸集，$x_0\in \partial C$，则存在 $a\ne 0$ 使得

$$a^Tx \le a^Tx_0,\forall x\in cl(C).$$ 注： 这时称超平面 $\mathcal{H} = \lbrace x| a^Tx = a^Tx_0\rbrace$ 是集合 $C$ 在 $x_0$ 处的支撑超平面。