這篇博客主要归纳总结凸集的相关基本概念和性质，主要参考 Stephen Boyd 的 Convex Optimization, 以及 Dimitri P.Bertsekas 的 Convex Analysis and Optimization 等教材。

一、凸集、凸组合和凸包

定义1.1（凸集） 设集合 \(C\subset \mathbb{R}^n\). 若 \(C\) 中任意两点所连的线段仍落在 \(C\) 中， 即对 \(\forall x_1, x_2 \in C\) 和 \(\forall \alpha \in [0,1]\), 都有 \[ \alpha x_1 + (1-\alpha) x_2 \in C,\] 则称 \(C\) 为 凸集(Convex Set)。
上述定义用图形直观描述如下：（左：凸集， 右：非凸）

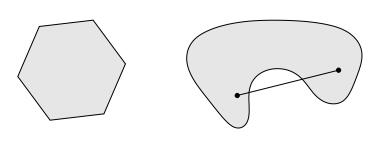
定义1.2（凸组合） 设集合 \(C\subset \mathbb{R}^n\). 称点 \(\sum\limits_{i=1}^k \alpha_i x_i\) 为 集合 \(C\) 中 \(x_1,x_2,\cdots,x_k\) 的一个 凸组合(Convex Combination)，其中 \(\alpha_i \ge 0,\ i=1,\cdots,k\) 并且 \(\sum\limits_{i=1}^k \alpha_i= 1\).
注：
1) 将凸集的定义1.1换种说法得，\(C\) 为凸集 当且仅当 \(C\) 包含其中任意两点的凸组合。
2) 通过归纳可得： 如果 \(C\) 为凸集，则 \(C\) 包含其中任意有限个点的凸组合。

定义1.3（凸包） 设集合 \(C\subset \mathbb{R}^n\). 集合 \(C\) 的 凸包(Convex Hull) 定义为 \(C\) 中任意有限个点的凸组合所构成的集合，记为 \(\mathrm{conv}(C)\): \[\mathrm{conv}(C) = \lbrace \sum_{i=1}^k \alpha_i x_i| x_i\in C, \alpha_i\ge 0, i=1,\cdots,k, \sum_{i=1}^k \alpha_i= 1,\forall k \in \mathbb{N}\rbrace.\] 凸包用图形直观理解如下：（左：十五个点构成集合的凸包， 右：肾形集合的凸包）

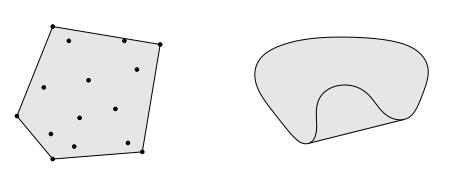
命题1.4（凸包的本质特征） 设集合 \(C\subset \mathbb{R}^n\),集合 \(C\) 的凸包 是 \(\mathbb{R}^n\) 包含 \(C\) 的所有凸集的交，即 \[\mathrm{conv}(C) = \bigcap\lbrace \mathcal{C}|\mathcal{C}\text{是凸集}, C\subset \mathcal{C}\rbrace\] 注：
1) 凸包 \(\mathrm{conv}(C)\) 总是凸的，不管 \(C\) 是否为凸；
2) 凸包 \(\mathrm{conv}(C)\) 是包含 \(C\) 的最小凸集, 从而若 \(C\) 是凸集，则 \(\mathrm{conv}(C) = C\).

二、保凸运算

这一部分描述一些保凸运算，利用这些运算可以简单验证一个集合是否是凸集，以及可以从一个凸集构造出其他凸集。
2.1 凸集的任意交是保凸的
对任意 \(\alpha\in \mathcal{I}\), \(C_\alpha\) 都是凸的，则 \(\cap_{\alpha\in\mathcal{I}}C_{\alpha}\) 也是凸集。

2.2 凸集的Cartesian积是保凸的
若 \(C_1\) 和 \(C_2\) 是凸集，则 \(C_1\times C_2 = \lbrace (x_1,x_2)|x_1\in C_1,x_2\in C_2\rbrace\) 也是凸集。

2.3 凸集在仿射运算下保凸（重要！！！）
函数 \(f: \mathbb{R}^n \rightarrow \mathbb{R}^m\) 是仿射的，若具有 \(f(x) = Ax + b\) 的形式，其中 \(A \in \mathbb{R}^{m\times n}\), \(b\in \mathbb{R}^m\).
设 \(C \subset \mathbb{R}^n\) 是凸集，
一方面，若 \(f: \mathbb{R}^n \rightarrow \mathbb{R}^m\) 是仿射函数， 则 \(C\) 在 \(f\) 下的像 \(f(C) = \lbrace f(x)|x\in C\rbrace\) 是凸的。
另一方面， 若 \(f: \mathbb{R}^k \rightarrow \mathbb{R}^n\) 是仿射函数, 则 \(C\) 在 \(f\) 下的原像 \(f^{-1}(C) = \lbrace x|f(x)\in C\rbrace\) 也是凸的.
注：在仿射运算下的保凸性质应用相当广泛。
简单例子:
1. 伸缩 若 \(C\in \mathbb{R}^n\) 是凸集, 以及 \(\alpha\in \mathbb{R}\), 则 \(\alpha C = \lbrace \alpha x|x\in C\rbrace\) 是凸集； {这里取 \(f(x) = \alpha x\) 即可}

2. 凸集的和 若 \(C_1\) 和 \(C_2\) 是凸集，则 \(C_1+ C_2 =\lbrace x_1 + x_2|x_1\in C_1,x_2\in C_2\rbrace\) 也是凸集。 {这里取 \(f(x_1,x_2) = x_1+x_2\), 则 \(f(C_1\times C_2) = C_1+C_2\)}

3. 平移 若 \(C\in \mathbb{R}^n\) 是凸集, 以及 \(a\in \mathbb{R}^n\), 则 \(C+a = \lbrace x+a|x\in C\rbrace\) 是凸集；{这里取 \(f(x) = x+a\) 即可}

4. 多面体 \(\mathcal{P} = \lbrace x|Ax \preceq b, Cx=d\rbrace\), 其中 \(A\in \mathbb{R}^{m\times n}\)
   分析： \(b-Ax \succeq 0, d-Cx=0\), 考虑 \(S= \mathbb{R}^m_+ \times \lbrace 0 \rbrace\), 仿射函数 \(f(x) = (b-Ax,d-Cx)\),
   则 \(f^{-1}(S) = \lbrace x|Ax \preceq b, Cx=d\rbrace\). 从而由于 \(S\) 是凸的， \(f\) 是仿射函数 ，则 \(\mathcal{P} = f^{-1}(S)\) 为凸。

5. 椭球 \(\mathcal{E} = \lbrace x| (x-x_c)^TP^{-1}(x-x_c)\le 1\rbrace\), 其中 \(P \succ 0\), 即 \(P\) 是对称正定矩阵。
   第一种思路： 考虑 \(S= \lbrace u| \lVert u \rVert_2 \le 1\rbrace\), 以及仿射函数 \(f(u) = P^{\frac12}u + x_c\), 则 \(f(S) = \lbrace x|(x-x_c)^TP^{-1}(x-x_c)\le 1\rbrace\);
   第二种思路： 由于 \((P^{-\frac{1}{2}}(x-x_c))^T(P^{-\frac{1}{2}}(x-x_c))\le 1\), 令 \(u = P^{-\frac{1}{2}}(x-x_c)\). 考虑 \(S= \lbrace u| \lVert u \rVert_2 \le 1\rbrace\)，以及仿射函数 \(g(x) = P^{-\frac{1}{2}}(x-x_c)\), 则 \(g^{-1}(S) = \lbrace x|(x-x_c)^TP^{-1}(x-x_c)\le 1\rbrace\).

注:
1) 由上述简单例子 1+2 可推出：若 \(C_1\) 和 \(C_2\) 是凸集，以及 \(\alpha,\beta\in \mathbb{R}\),则 \(\alpha C_1+ \beta C_2\) 也是凸集。
2) （凸集的部分和是凸集） 若 \(C_1\) 和 \(C_2\) 是 \(\mathbb{R}^{n}\times \mathbb{R}^m\) 中的凸集， 则部分和 \(S = \lbrace x,y_1+y_2|(x,y_1)\in C_1, (x,y_2)\in C_2\rbrace\) 也是凸集，其中 \(x\in \mathbb{R}^n，y_1,y_2\in \mathbb{R}^m\).
（证明思路：运用凸集的定义证明即可。）
若 \(m=0\) 时，上述部分和给出令 \(C_1\) 和 \(C_2\) 的交集； 若 \(n=0\) 时， 上述部分和给出 \(C_1\) 和 \(C_2\) 之和。

2.4 凸集拓扑性质
设集合 \(C\) 是凸集，则 \(C\) 的闭包 \(\mathrm{cl}(C)\) 和 内部 \(\mathrm{int}(C)\) 也是凸集。
注： 这里闭包和内部采用记号 \(\mathrm{cl}(C)\) 和 \(\mathrm{int}(C)\)，而不是记号 \(\overline{C}\) 和 \(C^o\)，主要是为了行文方便。